Ejemplos
lunes, 16 de noviembre de 2015
Topología
TOPOLOGÍA
Históricamente, las Primeras Ideas topológicas conciernen al Concepto de Límite y al de completitud de la ONU espacio métrico, y se manifestaron Principalmente en la crisis de los inconmesurables de los pitagóricos, ante la Aparición de Números Reales no racionales. El Primer acercamiento concreto al Concepto de Límite y también al de integrante Aparece En El Método de exhaución de Arquímedes. La Aparición del Análisis Matemático en el siglo XVII Puso en Evidencia la Necesidad de formalizar los Conceptos de Proximidad y Continuidad, y La Incapacidad de la geometría párrafo TRATAR Este tema. Fue Precisamente la fundamentación del Cálculo infinitesimal, Asi Como los Intentos de formalizar el Concepto de Variedad en Geometría Lo Que Llevo a la Aparición de la topología, una los finales del siglo XIX y Principios del XX.
Se Suele fechar el origen de la topología con la Resolución por parte de Euler del Problema de los puentes de Königsberg, en 1735. Ciertamente, la Resolución de Euler del Problema utilizació Una forma de Pensar Totalmente topológica, y La Solución del Problema nos Lleva un La Característica de Euler, el cebador invariante de la topología algebraica, Pero seria muy arriesgado y arbitrario fechar en ESE Momento la Aparición de la topología. La Situación es exactamente análoga a la del Cálculo del área de la elipse por Arquímedes.
El término topología FUE USADO por Primera Vez por Johann Benedict Listing, en 1836 del una carta a su antiguo profesor de la Escuela Primaria, Müller, y posteriormente en su libro Vorstudien zur Topologie ('Estudios Previos a la topología'), publicado en 1847 . Anteriormente se la denominaba análisis situs. Maurice Fréchet introdujo el Concepto de espacio métrico en 1906.
R ama de las matemáticas Dedicada al estudio de Aquellas propiedades de los cuerpos Geométricos Que permanecen inalteradas por Transformaciones CONTINUAS. Es Una Disciplina Que ESTUDIA las Propiedades de los Espacios topológicos y Las última Voluntad CONTINUAS. La topología se Interesa por Conceptos de Como Proximidad, Número de AGUJEROS, el tipo de Consistencia (o textura) Que Presenta Objeto ONU, Comparación de Objetos y Clasificar Múltiples Atributos Donde Destacanconectividad, compacidad, metricidad o metrizabilidad, Entre Otros.
martes, 10 de noviembre de 2015
Estadística y Probabilidad
ESTADÍSTICA Y PROBABILIDAD
Perdomo. K. (2013, Mayo 11) .Probabilidad. Recuperado de http://es.slideshare.net/karlaperdomo/probabilidad-23474720
Análisis Complejo
ANÁLISIS COMPLEJO
El análisis complejo (o teoría de las funciones de variable compleja) es la rama de las matemáticas que en parte investiga lasfunciones holomorfas, también llamadas funciones analíticas. Una función es holomorfa en una región abierta del plano complejo si está definida en esta región, toma valores complejos y por último es diferenciable en cada punto de esta región abierta con derivadas continuas.
El que una función compleja sea diferenciable en el sentido complejo tiene consecuencias mucho más fuertes que la diferenciabilidad usual en los reales. Por ejemplo, toda función holomorfa se puede representar como una serie de potencias en algún disco abierto donde la serie converge a la función. Si la serie de potencias converge en todo el plano complejo se dice que la función es entera. Una definición relacionada con función holomorfa es función analítica: una función compleja sobre los complejos que puede ser representada como una serie de potencias. De modo que toda función holomorfa también cumple la definición de función analítica pero no toda función analítica es holomorfa. En particular, las funciones holomorfas son infinitamente diferenciables, un hecho que es marcadamente diferente de lo que ocurre en las funciones reales diferenciables. La mayoría de las funciones elementales como lo son, por ejemplo, algunos polinomios, la función exponencial y las funciones trigonométricas, son holomorfas.

Gráfico de la función f(z)=(z2-1)(z-2-i)2/(z2+2+2i). La coloración representa elargumento de la función, mientas que el brillo representa el módulo.
Resultados
Integrales de contorno
Series de Laurent
Teorema de Liouville
Continuación analítica
Recuperado de: https://es.wikipedia.org/wiki/An%C3%A1lisis_complejo
Rigor En El Análisis
RIGOR EN EL ANÁLISIS

- El rigor en matemáticas nació con Augustin-Louis Cauchy.
- Cauchy trató de establecer una base rigurosa para el análisis matemático.
- Un buen ejemplo fue su demostración del teorema del valor intermedio, que afirma que toda función real f(x) continua en un intervalo [a,b] asume cada valor posible entre f(a) y f(b) en ese intervalo.
- Cauchy enseñó la demostración de este teorema por primera vez en el curso que impartió en la École Royale Polytechnique en 1816.
- Su libro de texto de 1821, admirado por más de una generación de matemáticos, presenta dos demostraciones diferentes; la más famosa, la que todos los estudiantes de matemáticas aprenden, fue relegada a un apéndice. Nos lo recuerda Michael J. Barany, “Stuck in the Middle: Cauchy’s Intermediate Value Theorem and the History of Analytic Rigor,”
- Cauchy fue un profesor impopular tanto entre los estudiantes como entre sus compañeros de facultad. Sus clases eran muy densas y difíciles de seguir, muchas veces prolongaba la clase más allá de su horario oficial y además realizaba continuas revisiones del temario.
- Cauchy asume que todas las funciones continuas son diferenciables. Sin embargo, lo importante del proyecto de reforma del análisis iniciado por Cauchy, que trata de llevar el rigor al análisis de la mano de la geometría y del álgebra, es que inició un camino hacia el rigor cuya culminación fue el motor de gran parte de la matemática de todo el siglo XIX, con la honrosa excepción del genial Henri Poincaré que vio en el rigor un corsé del que había que deshacerse.
- El cénit del rigor en las matemáticas llegó en el siglo XX con Nicolas Bourbaki, el nombre colectivo de un grupo de matemáticos franceses que, en los años 1930, se pusieron a revisar todos los fundamentos de las matemáticas con una exigencia absoluta en el rigor tratando de combatir la corriente que había nacido con Poincaré. Matemáticos como Jean Dieudonné, André Weil, Henri Cartan, Claude Chevalley, y otros antiguos alumnos de la Escuela Normal Superior de París recogieron el guante de Cauchy e impusieron a toda la matemática el concepto de rigor matemático como definición de la labor del matemático.
Un matemático es una máquina de demostrar teoremas con absoluto rigor. La máxima revolucionaria de Bourbaki es Vive la rigueur!
Recuperado de: http://francis.naukas.com/2013/10/27/cauchy-y-el-rigor-en-el-analisis-matematico/
lunes, 9 de noviembre de 2015
Matrices
MATRICES

Una matriz es un arreglo bidimensional de números (llamados entradas de la matriz) ordenados en filas (o renglones) y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con n filas y m columnas se le denomina matriz n-por-m (escrito  ) donde
) donde 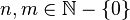 . El conjunto de las matrices de tamaño
. El conjunto de las matrices de tamaño  se representa como
se representa como  , donde
, donde  es el campo al cual pertenecen las entradas. El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después.
es el campo al cual pertenecen las entradas. El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después.
 ) donde
) donde 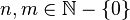 . El conjunto de las matrices de tamaño
. El conjunto de las matrices de tamaño  se representa como
se representa como  , donde
, donde  es el campo al cual pertenecen las entradas. El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después.
es el campo al cual pertenecen las entradas. El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después.
Dos matrices se dice que son iguales si tienen el mismo tamaño y los mismos elementos en las mismas posiciones.
A la entrada de una matriz que se encuentra en la fila 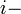 ésima y la columna
ésima y la columna 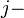 ésima se le llama entrada
ésima se le llama entrada  o entrada
o entrada 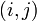 -ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnas.
-ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnas.
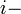 ésima y la columna
ésima y la columna 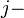 ésima se le llama entrada
ésima se le llama entrada  o entrada
o entrada 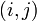 -ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnas.
-ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnas.
Se denota a las matrices con letra mayúscula, mientras que se utiliza la correspondiente letra en minúsculas para denotar a las entradas de las mismas, con subíndices que refieren al número de fila y columna del elemento.4 Por ejemplo, al elemento de una matriz  de tamaño
de tamaño  que se encuentra en la fila
que se encuentra en la fila 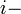 ésima y la columna
ésima y la columna 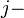 ésima se le denota como
ésima se le denota como 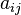 , donde
, donde 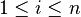 y
y 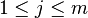 .
.
 de tamaño
de tamaño  que se encuentra en la fila
que se encuentra en la fila 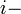 ésima y la columna
ésima y la columna 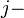 ésima se le denota como
ésima se le denota como 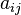 , donde
, donde 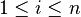 y
y 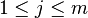 .
.
Cuando se va a representar explícitamente una entrada la cuál está indexada con un 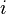 o un
o un  con dos cifras se introduce una coma entre el índice de filas y de columnas. Así por ejemplo, la entrada que está en la primera fila y la segunda columna de la matriz
con dos cifras se introduce una coma entre el índice de filas y de columnas. Así por ejemplo, la entrada que está en la primera fila y la segunda columna de la matriz  de tamaño
de tamaño 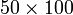 se representa como
se representa como 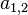 mientras que la entrada que está en la fila número 23 y la columna 100 se representa como
mientras que la entrada que está en la fila número 23 y la columna 100 se representa como 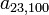 .
.
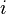 o un
o un  con dos cifras se introduce una coma entre el índice de filas y de columnas. Así por ejemplo, la entrada que está en la primera fila y la segunda columna de la matriz
con dos cifras se introduce una coma entre el índice de filas y de columnas. Así por ejemplo, la entrada que está en la primera fila y la segunda columna de la matriz  de tamaño
de tamaño 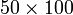 se representa como
se representa como 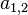 mientras que la entrada que está en la fila número 23 y la columna 100 se representa como
mientras que la entrada que está en la fila número 23 y la columna 100 se representa como 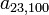 .
.
Además de utilizar letras mayúsculas para representar matrices, numerosos autores representan a las matrices con fuentes en negrita para distinguirlas de otros objetos matemáticos.[cita requerida] Así  es una matriz, mientras que
es una matriz, mientras que  es un escalar en esa notación. Sin embargo esta notación generalmente se deja para libros y publicaciones, donde es posible hacer esta distinción tipográfica con facilidad. En otras notaciones se considera que el contexto es lo suficientemente claro como para no usar negritas.
es un escalar en esa notación. Sin embargo esta notación generalmente se deja para libros y publicaciones, donde es posible hacer esta distinción tipográfica con facilidad. En otras notaciones se considera que el contexto es lo suficientemente claro como para no usar negritas.
 es una matriz, mientras que
es una matriz, mientras que  es un escalar en esa notación. Sin embargo esta notación generalmente se deja para libros y publicaciones, donde es posible hacer esta distinción tipográfica con facilidad. En otras notaciones se considera que el contexto es lo suficientemente claro como para no usar negritas.
es un escalar en esa notación. Sin embargo esta notación generalmente se deja para libros y publicaciones, donde es posible hacer esta distinción tipográfica con facilidad. En otras notaciones se considera que el contexto es lo suficientemente claro como para no usar negritas.
Otra notación, en sí un abuso de notación, representa a la matriz por sus entradas, i.e. 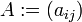 o incluso
o incluso 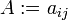 .
.
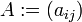 o incluso
o incluso 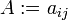 .
.
Como caso particular de matriz, se definen los vectores fila y los vectores columna. Un vector fila o vector renglón es cualquier matriz de tamaño  mientras que un vector columna es cualquier matriz de tamaño
mientras que un vector columna es cualquier matriz de tamaño 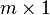 .
.
 mientras que un vector columna es cualquier matriz de tamaño
mientras que un vector columna es cualquier matriz de tamaño 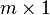 .
.
A las matrices que tienen el mismo número de filas que de columnas, 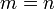 , se les llama matrices cuadradas y el conjunto se denota
, se les llama matrices cuadradas y el conjunto se denota 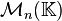 , alternativamente a la notación usual
, alternativamente a la notación usual  .
.
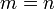 , se les llama matrices cuadradas y el conjunto se denota
, se les llama matrices cuadradas y el conjunto se denota 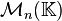 , alternativamente a la notación usual
, alternativamente a la notación usual  .
.Álgebra Simbólica
ÁLGEBRA SIMBÓLICA
Durante el siglo XVIII se continuó trabajando en la teoría de ecuaciones y en 1799 el matemático alemán Carl Friedrich Gauss publicó la demostración de que toda ecuación polinómica tiene al menos una raíz en el plano de los números complejos.
En los tiempos de Gauss, el álgebra había entrado en su etapa moderna. El foco de atención se trasladó de las ecuaciones polinómicas al estudio de la estructura de sistemas matemáticos abstractos, cuyos axiomas estaban basados en el comportamiento de objetos matemáticos, como los números complejos, que los matemáticos habían encontrado al estudiar las ecuaciones polinómicas.
Dos ejemplos de dichos sistemas son los grupos y las cuaternas, que comparten algunas de las propiedades de los sistemas numéricos, aunque también difieren de ellos de manera sustancial.
Los grupos comenzaron como sistemas de permutaciones y combinaciones de las raíces de polinomios, pero evolucionaron para llegar a ser uno de los más importantes conceptos unificadores de las matemáticas en el siglo XIX.
Los matemáticos franceses Galois y Augustin Cauchy, el británico Arthur Cayley y los noruegos Niels Abel y Sophus Lie hicieron importantes contribuciones a su estudio.
Las cuaternas fueron descubiertas por el matemático y astrónomo irlandés William Rowan Hamilton, quien desarrolló la aritmética de los números complejos para las cuatreñas.
Después del descubrimiento de Hamilton el matemático alemán Hermann Grassmann empezó a investigar los vectores. A pesar de su carácter abstracto, el físico estadounidense J. W. Gibbs encontró en el álgebra vectorial un sistema de gran utilidad para los físicos, del mismo modo que Hamilton había hecho con las cuaternas.
La amplia influencia de este enfoque abstracto llevó a George Boole a escribir Investigación sobre las leyes del pensamiento (1854), un tratamiento algebraico de la lógica básica. Desde entonces, el álgebra moderna —también llamada álgebra abstracta— ha seguido evolucionando; se han obtenido resultados importantes y se le han encontrado aplicaciones en todas las ramas de las matemáticas y en muchas otras ciencias.
Recuperado de:
Recuperado de:
http://www.profesorenlinea.cl/matematica/AlgebraHistoria.htm
Álgebra Moderna O Álgebra Abstracta
ÁLGEBRA MODERNA O ÁLGEBRA ABSTRACTA
álgebra abstracta se desarrolló en el siglo XIX, inicialmente centrada en lo que hoy se conoce como teoría de Galois y en temas de la constructibilidad.12 Los trabajos de Gauss generalizaron numerosas estructuras algebraicas. La búsqueda de una fundamentación matemática rigurosa y una clasificación de los diferentes tipos de construcciones matemáticas llevó a crear áreas del álgebra abstracta durante el siglo XIX absolutamente independientes de nociones aritméticas o geométricas (algo que no había sucedido con el álgebra de los siglos anteriores).
Consiste en que los números se emplean para representar cantidades conocidas y determinadas. Las letras se emplean para representar toda clase de cantidades, ya sean conocidas o desconocidas. Las cantidades conocidas se expresan por las primeras letras del alfabeto: a, b, c, d, … Las cantidades desconocidas se representan por las últimas letras del alfabeto: u, v, w, x, y, z.
Los signos empleados en álgebra son tres clases: Signos de operación, signos de relación y signos de agrupación.
Signos de operación
En álgebra se verifican con las cantidades las mismas operaciones que en aritmética: suma, resta, multiplicación, elevación a potencias y extracción de raíces, que se indican con los principales signos de aritmética excepto el signo de multiplicación. En lugar del signo × suele emplearse un punto entre los factores y también se indica a la multiplicación colocando los factores entre paréntesis. Así a⋅b y (a)(b) equivale a a × b.
Signos de relación
Se emplean estos signos para indicar la relación que existe entre dos cantidades. Los principales son: =, que se lee igual a. Así, a=b se lee “a igual a b”. >, que se lee mayor que. Así, x + y > m se lee “x + y mayor que m”. <, que se lee menor que. Así, a < b + c se lee “a menor que b + c”.
Signos de agrupación
Los signos de agrupación son: el paréntesis ordinario ( ), el paréntesis angular o corchete [ ], las llaves { } y la barra o vínculo ||. Estos signos indican que la operación colocada entre ellos debe efectuarse primero. Así, (a + b)c índica que el resultado de la suma a y b debe multiplicarse por c; [a – b]m indica que la diferencia entre a y b debe multiplicarse por m, {a + b} ÷ {c – d} índica que la suma de a y b debe dividirse entre la diferencia de c y d. El orden de estos signos son de la siguiente forma { [ ( ) ] }, por ejemplo: { [ (a + b) - c] ⋅ d} indica que al resultado de la suma de a + b debe restarse c y el resultado de esto multiplicarse por d.
Teoría De Números
TeoríA De NúMeros from Marcel Ruiz
Recuperado de: http://es.slideshare.net/marcelruiz/teora-de-nmeros-presentation
Recuperado de: http://es.slideshare.net/marcelruiz/teora-de-nmeros-presentation
domingo, 8 de noviembre de 2015
Probabilidad
Historia De La Probabilidad from gachea
Recuperado de:
http://es.slideshare.net/gachea/historia-de-la-probabilidad-1476170
sábado, 7 de noviembre de 2015
Geometría
Geometria .... mirian rios mtz... 212 from Arte Diseño
Recuperado de:
http://es.slideshare.net/rociogamba50/geometria-mirian-rios-mtz-212-45157866
Recuperado de:
http://es.slideshare.net/rociogamba50/geometria-mirian-rios-mtz-212-45157866
martes, 3 de noviembre de 2015
Matemática En El Renacimiento (Álgebra, Trigonometría, Geometría, Astronomía y Mecánica
Matemática en el Renacimiento from Alejandra Agreman
Recuperado De: http://es.slideshare.net/AlejandraAgreman/matemtica-en-el-renacimiento
Recuperado De: http://es.slideshare.net/AlejandraAgreman/matemtica-en-el-renacimiento
El Álgebra En El Renacimiento.
El Álgebra en el Renacimiento
- Durante el Renacimiento las actividades matemáticas lograron avances muy importantes en el campo del álgebra, la trigonometría y la geometría.
- Ya se utiliza un simbolismo rudimentario en álgebra, lo símbolos indo-arábigos están suficientemente extendidos, las fracciones decimales se desarrollan poco a poco y la teoría de las ecuaciones ha logrado comprender la solución general de la cúbica y la bicuadrática.
- Los números negativos se aceptan progresivamente y la trigonometría, considerada ciencia independiente, dispone ya de tablas muy precisas para las seis funciones. En cuanto a la geometría, se desarrollan nuevas orientaciones en geometría descriptiva y proyectiva. Todos estos avances son ampliamente difundidos de forma más normalizada gracias a la imprenta.
- La aplicación de todos estos conocimientos a campos tan diversos como la cartografía, el arte, la óptica o la contabilidad sirvió para relanzar las matemáticas y darles un impulso de modernidad, con un sentido más crítico de los modelos clásicos, intentando definir otros nuevos que los sustituyeran.
- A esta etapa de la culminación del Renacimiento y comienzo de las matemáticas modernas contribuyó de forma especial François Viète.
- El álgebra hasta el siglo XVI era de tipo verbal, en realidad, el álgebra todavía estaba en ese tiempo muy conectada con la geometría. La incógnita de un problema era pensada como la longitud de un segmento de recta; el cuadrado de la incógnita se refería al área de un cuadrado y su cubo, al volumen de un cubo.
François Viète
Conocido en textos en españoles por su nombre latinizado Francisco Vieta., matemático francés, nace en Fontenay-le-Comte, Francia en el año 1540 y murió en París Francia, en el año 1603).
Suscribirse a:
Comentarios (Atom)




